Abu Rayhan Muhammad ibn Ahmad al-Biruni (973 bis zirka 1050) ermittelte 1023 mit einem von ihm erfundenen Verfahren den Radius der Erdkugel und kam mit 6339,6 Kilometern auf 2,6 ‰ genau hin (heute: 6371 km)!
Hier seine Methode
(gute Quelle https://en.wikipedia.org/wiki/History_of_geodesy#Islamic_world : In contrast to his predecessors who measured the Earth’s circumference by sighting the Sun simultaneously from two different locations, Al-Biruni developed a new method of using trigonometric calculations based on the angle between a plain and mountain top which yielded more accurate measurements of the Earth’s circumference and made it possible for it to be measured by a single person from a single location.[12][13][14] Al-Birun’s method’s motivation was to avoid “walking across hot, dusty deserts” and the idea came to him when he was on top of a tall mountain in India (present day Pind Dadan Khan, Pakistan).[14] From the top of the mountain, he sighted the dip angle which, along with the mountain’s height (which he calculated beforehand), he applied to the law of sines formula. This was the earliest known use of dip angle and the earliest practical use of the law of sines.[13][14]
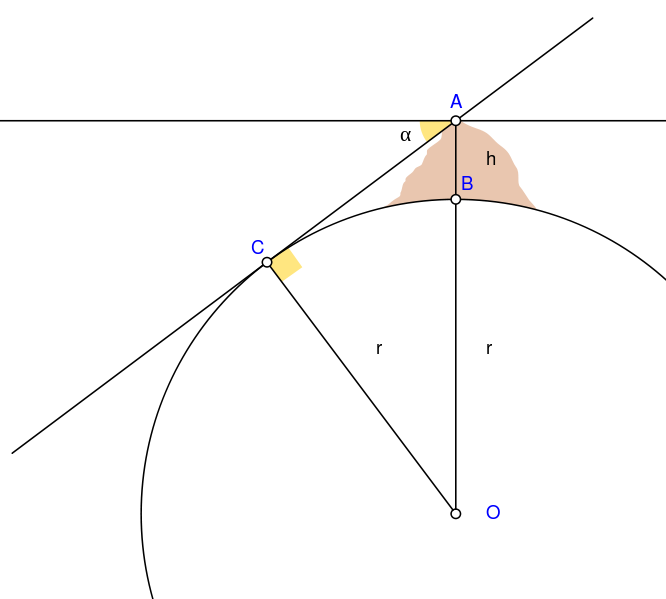Erstmals wurde der Sinus beziehungsweise Cosinus verwendet, vom Neigungswinkel α zwischen der Horizontalen (durch A, die Bergspitze) und der wahren Horizontrichtung zu C. Weil α + ∠CAB = 90° sind und im rechtwinkligen Dreieck AOC auch ∠CAB + ∠AOC = 90°, muss auch der Winkel ∠AOC = α sein. Erdradius + Bergeshöhe, r+h OA bildet im Dreieck AOC die Hypothenuse. Gratulation Biruni!
Im Wikipedia-Diagramm-Original:
Biruni (973 - 1048) developed a new method using trigonometric
calculations to compute earth's radius and circumference based on the
angle between the horizontal line and true horizon from a mountain top
with known height. He calculated the height of the mountain by going to
two points at sea level with a known distance apart and then measuring
the angle between the plain and the top of the mountain for both points.
Biruni's estimate of 6,339.9 km for the Earth radius had an error of 0.0026 [2.6 ‰] and was 16.8 km less than the current value of 6,356.7 km. The idea came to him when he was on top of a tall mountain near Nandana in India. He measured the dip angle using an astrolabe and he applied to the law of sines formula. He also made use of algebra in his calculation.
- A = Highest point of mountain
- B = Lowest point of mountain
- h = Height of the mountain
- C = Lowest point of true horizon visible from point A
- O = Centre of Earth
- α = Dip angle
- r = Earth's radius
The angle AOC = α.
AO=(r+h) is the hypotenuse in triangle AOC.
r=(r+h).cos(α)
Then the right side can be simplified to find r.
r=h.cos(α)/(1-cos(α))
Steht hier: https://commons.wikimedia.org/wiki/File:Abu_Reyhan_Biruni-Earth_Circumference.svg
Link hierher: http://j.mp/2MSN2m5
= https://blogabissl.blogspot.com/2019/10/wie-biruni-1023-den-erdradius-auf-26.html
Keine Kommentare:
Kommentar veröffentlichen