Ein Viereck sind vier Punkte – auf einer Ebene! – die mit Geraden verbunden sind und eine Fläche bilden. Engl. quadrileteral,quadrangle, tetragon. Ein ✕ ist kein Viereck!
 |
| Aus dem Bronstein |
Das beliebteste Rechteck ist ein Quadrat, □, oben Abb. 2.18. Engl. square, wie auch ein Platz in einer Stadt. Es ist ein Rechteck mit vier gleich langen Seiten. Beispiel: die Kästchen im Rechenheft. Wieder: Ein Quadrat ist ein Rechteck, ein Rechteck ist aber kein Quadrat.
Quetscht man ein Rechteck so, dass immer zwei gegenüberliegende Seiten parallel sind, dann ist ein Parallogramm, engl. paralellogram mit einem m.
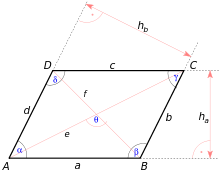 |
| Parallelogramm in der Wikipedia |
.svg/1000px-Flag_of_Bavaria_(lozengy).svg.png) |
| Die Bayrische Flagge besteht aus Rauten. |
Die Raute (oder der Rhombus), oben Abb. 2.19, engl. rhombus, sieht aus wie ein Drachen, ist ein Parallelogramm mit vier gleich langen Seiten. Die Querverbindungen gegenüberliegender Punkte (»Diagonalen«) schneiden sich senkrecht. Ist ein Quadrat eine Raute? Gibt’s auch auf einer Spielkarte.
Ein Trapez – bekannt aus dem Zirkus – ist ein Viereck mit zwei parallelen Seiten, natürlich gegenüberliegenden, oben Abb. 2.20. Schön sieht das nicht aus. Ein gleichschenkeliges Trapez dagegen sieht ordentlicher aus.
Hier, wieder aus der Wikipedia, die ganze Viereckfamilie, dort sogar klickbar:
Übrigens: Konvex ist nach außen gebeult, konkav das Gegenteil, hier gibt’s dazu Merksätze.
Außerdem erfährt man:
• Quadrate ⊂ Rechtecke ⊂ Parallelogramme ⊂ Trapeze ⊂ konvexe Vierecke
• Quadrate = Rechtecke ∩ Rauten
• Quadrate = Drachenvierecke ∩ gleichschenklige Trapeze
• Rechtecke = Sehnenvierecke ∩ Parallelogramme
• Rauten = Drachenvierecke ∩ Trapeze
• Rauten = Tangentenvierecke ∩ Parallelogramme
• Gleichschenklige Trapeze = Sehnenvierecke ∩ Trapeze
Und lernt so, dass ⊂ heißt: eine Unter- oder Teilmenge von, das ∩ besagt, dass zwei Dinge eine Schittmenge bilden:
Genug.
Link hierher:
http://blogabissl.blogspot.com/2016/04/vierecke.html


Keine Kommentare:
Kommentar veröffentlichen