√2 < 2 < e < 3 < π
Und so weiter mit beliebigen Beispielen. Zahlen sind skalare Größen, jedenfalls »reele« Zahlen, wie eine Temperatur, ein Blutdruck oder dergleichen. Erst »komplexe« Zahlen haben zwei Bestimmungsgrößen, und lassen sich deshalb nicht so einfach vergleichen, ebenso Vektoren und höhere mathematische Gebilde wie Tensoren etc. Mir geht’s nur um Skalare, wo es ein einfaches Größer und Kleiner gibt.
Und da hat mich jüngst ein Schüler der siebten Klasse in Verlegenheit gebracht. Er meinte, -5 sei größer als -3. Nicht unvernünftig: Fünf Euro Schulden sind mehr als nur drei, das meinen auch andere. Ich hab’ dann schnell versucht, in seinem Matheheft die Definition zu finden, dann in seinem Buch, zuletzt in der Wikipedia, er aber wollte seine Hausaufgaben machen, war in Eile. Weil’s aber so richtig nirgends seht, haben wir dann tapfer mit der Annahme gerechnet: »Mehr weniger ist mehr«, was eine Zeit lang durchaus ging. Man muss das nur so definieren.
Bald aber merkte ich, dass unsere Definition unpraktisch war. Man sollte doch, wie bei normalen »Istgleich-Gleichungen« auch, rechts und links dasselbe zu- oder abziehen können, ohne dass sich das Zeichen (<, > oder =) ändern muss. Also:
Wenn a < b muss auch a + c < b + c sein, mit c als Konstante.
Und das geht nur, wenn auch zum Beispiel -3 < -2 und dann -3 +5 < -2 + 5 ist.
Definiert man falsch mit -3 > -2 wäre -3 + 5 > -2 + 5 oder +2 > +3, was nicht stimmt.
Also gelten die Regeln einer Gleichung immer auch bei Ungleichungen? Nicht ganz: Multipliziert man beide Seiten mit einer negativen Zahl, so drehen sich die Ungleichzeichen um, größer wird zu kleiner und umgekehrt:
2 < 3, rechts und links | × (-1), so wird -2 > -3.
(Bei unserer falschen Definition wäre das nicht so gewesen, dafür hätten aber alle anderen Regeln nicht geklappt.)
Genug gespielt. Wie definiere ich nun aber, sagen wir, das Kleiner-Zeichen < ? Ich würde sagen:
Man ordnet die Zahlen auf der Zahlengeraden, was weiter links ist, ist kleiner.
| Ich klaue mir dafür hier mal ein Stück Zahlengerade aus der Wikipedia. |
»Richtigen« Mathematikern widerstrebt das allerdings; warum, weiß ich nicht. Ersatzweise und notfalls würde ich eine arithmetische Hilfsdefinition nehmen, eben die praktische Tatsache, dass man rechts und links eine Konstante addieren kann, und das Ergebnis bleibt gleich. Diese Eigenschaft, und dass > das Gegenteil von < ist, das müsste reichen. Schön finde ich diese Definition nicht, die sozusagen hinterrücks über eine Eigenschaft die Sache veranschaulicht. Da könnte ich gleich eine Schubkarre als Tragbahre definieren, die statt mit zwei mit einem Träger auskommt.
Und da habe ich mich lang mit den Wikipedisten gestritten. Weil sie die reelen Zahlen nur als eine mögliche Sammlung von ganzen Zahlen, Bruchzahlen und sogar irrationalen Zahlen sehen, definieren sie für all diese Varianten reeller Zahlen größer und kleiner immer wieder leicht anders, als ob es darauf ankäme, die Zahlengerade proppenvoll zu machen. Und wenn dann wer eine natürliche Zahl – das sind die, die man beim Zählen bekommt – gar mit einer irrationalen vergleichen will – das sind die, die nie enden – dann passt keine Definition so recht, obwohl der Vergleich vielleicht ziemlich offensichtlich ist, etwa zwischen 3 und π.
Die Wikipedia-Defintion finden Sie hier:
Die Zahlen:
Symbol
|
Beispiel
|
HTML
|
Unicode
|
|
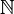 |
(0), 1, 2, 15, 348
|
&#x2115;
|
U+2115 |
|
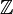 |
-31, -30, 0, 12, 122
|
&#x2124;
|
U+2124 |
|
|
|
-1/2, 7/8
|
Bruchzahl*) |
&#x1D539;
|
U+1D539 |
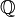 |
&#x211A;
|
U+211A |
||
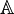
|
√2, √-2, (nicht π)
|
&#x1D538;
|
U+1D538 |
|

|
… inkl. π, e
|
&#x211D;
|
U+211D |
|
 |
(a+bi)
|
&#x2102;
|
U+2102 |
|
 |
(a+bi+cj+dk)
|
&#x210D;
|
U+210D |
*) »Bruchzahlen«, also Brüche aller Art, gehören zu den rationalen Zahlen (ratio = Bruch, Verhältnis). Dezimal können sie immer als endlich lange oder peridische Zahlen dargestellt werden.
+) Algebraische Zahlen sind nicht als Bruchzahl, und dezimal weder als periodische noch endlich lange Zahl darstellbar. Wikipedia: »Gegen Ende des 19. Jahrhunderts wurde bewiesen, dass die Kreiszahl π und die Eulersche Zahl e nicht algebraisch sind. Von anderen Zahlen, wie zum Beispiel π + e weiß man bis heute nicht, ob sie algebraisch oder transzendent sind. Siehe dazu den Artikel Transzendente Zahl.« Beispiele transzender Zahlen: π, e, sin(1).
 |
Größer in »Mathematik-Wissen«.
Link zu »Vergleichszeichen«.
Berühmte Ungleichungen.
Inzwischen schreibt Edward Frenkel in seinem Bestseller aus dem Jahr 2013 Love and Math (Seite 160): »Functions were, if you will, the concepts of archaic math, and sheaves [dt. Garben] are the concepts of modern math.« Übrigens ein Buch, das ich sehr empfehlen kann. Wie bei einem guten Krimi ist’s sehr spannend, obwohl man nicht gleich alles versteht. Ich fand besonders den Blick hinter den eisernen Vorhang interessant, nicht nur die Mathematik, die immer mehr von Einzelerscheinungen weg zu Gruppen, Feldern, Mengen kommt – ganz laienhaft empfunden. »In modern math there are concepts and ideas thet are deeper and more versatile: vector spaces, symmetry groups, arithmetic modulo prime numbers, sheaves« (p. 184). Meine »höhere Mathematik« ist allerdings nie über Ingenieurmathematik hinausgekommen, und auch dort nicht sehr weit: »Theoretische Elektrotechnik befriedigend«. – Hier die Buchkritik der Sunday Times.
Frenkels »Formula of Love«, Seite 238, aus http://arxiv.org/pdf/1211.3704.pdf#page=4
Und hier ein Bericht des französischen Fernsehens über den Film »Rites of Love an Math« von Reine Graves und Edward Frenkel:
PS am 22.März. Frenkels »Love and Math« nun ausgelesen. Der Anhang ist so umfangreich (ein Buch für sich), dass der Band gar nicht so dick ist, wie es sich anfühlt. Sehr überzeugend endet er mit der Erkenntnis, dass von den drei »tief verwobenene« Welten, der physikalischen, der geistigen und der »platonischen« der Mathematik – d. h. die der unabhängigen, abstrakten Wahrheiten – die letztere übersehen wird: »Many of us remain blissfully ignorant of the world of mathematics« [Seite 235 Mitte]. Wieder divine Wahrheiten zu fühlen, ist das Erlebnis seines Buches. (So zitiert er Heinrich Hertz [p 233]: »Man wird das Gefühl nicht los, dass diese mathematischen Formeln eine unabhängige Existenz und ihre eigene Intelligenz haben, dass sie gescheiter als wir sind, ja sogar gescheiter als ihre Entdecker, dass wir mehr aus ihnen errechnen, als wir ursprünglich hineinlegten.«
Wer nicht gleich baden will in Mathematik (oder »baden gehen«?), dem empfehle ich einen anregenden Blick auf die Geschichte der Zahlen, vielleicht gleich mit der Null beginnend.
| Aus http://www.zaubereinmaleins.de/kommentare/rechenplakate-groesser-als-kleiner-als....510/ von »Frau Wulf« |
Wenn wir schon beim Rechnen sind: 25 : 5 = 14 (englisch):
– Hilfe! Vorgestern fragte mich mein Schüler, warum Minus mal Minus Plus geben kann, wo doch beides im Minus ist. Dieses - · - = + ging ihm sichtlich gegen den Verstand. Ich konterte mit: »Wer sagt, er hätte nicht nicht gelogen, hat doch gelogen«, und damit, dass Malnehmen wie Dividieren ist, vom Vorzeichen her jedenfalls, und man dann schön das Minus wegkürzen kann:
- 4 4
—— = ——
- 2 2
Ich bin halt ein Fan von Brüchen und Kürzen.


1 Kommentar:
In GB wurden wir vor 60 Jahren gelehrt : in Bezug auf die Zahlengerade, dass < bedeutet 'links von' und > bedeutet 'rechts von', eine Eselbrücke die ich bis heute behalten habe :-)
Ich werde die Empfehlung für das Buch aufgreifen.
Kommentar veröffentlichen